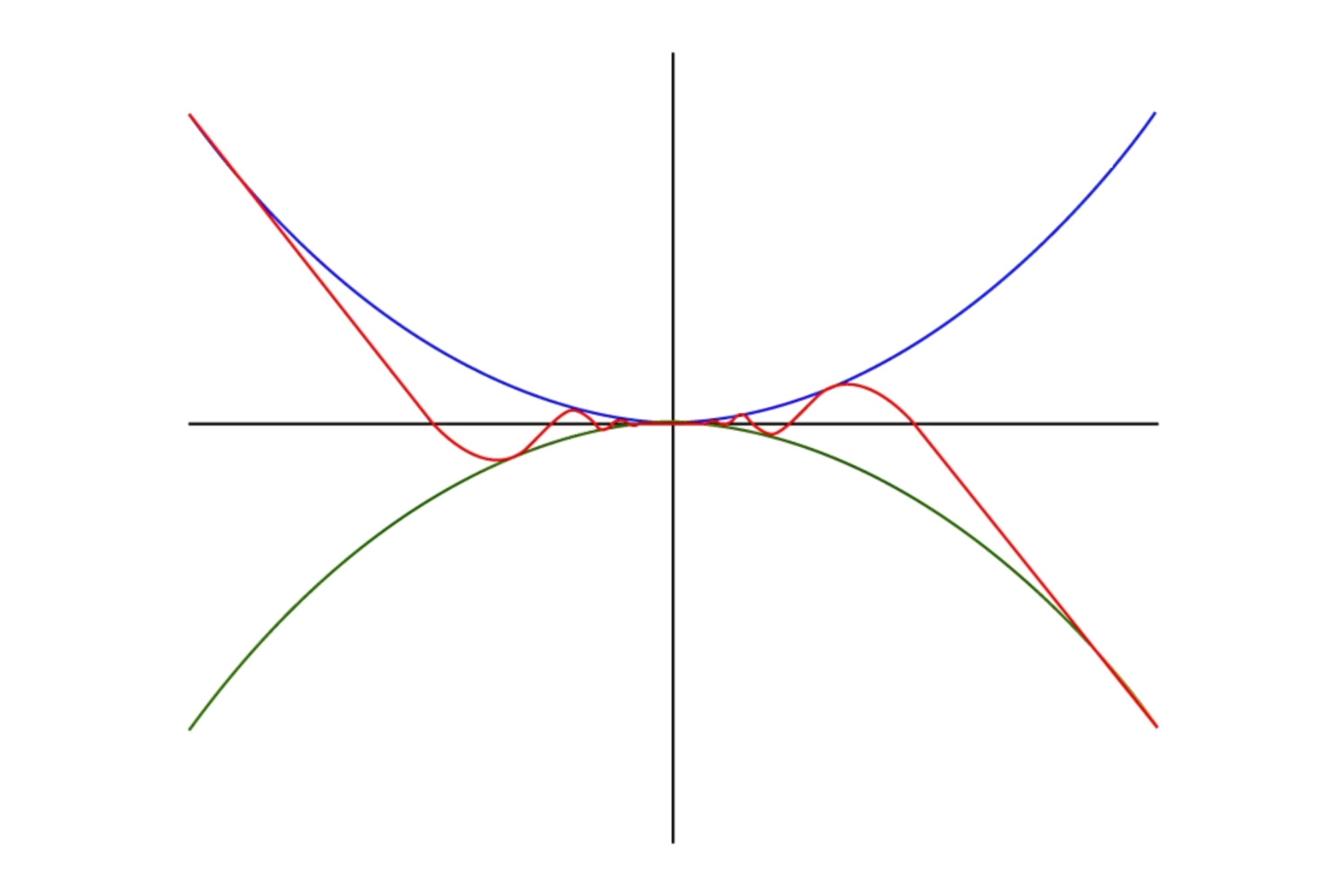
The Squeeze Theorem, also known as the Sandwich Theorem, is a powerful tool in calculus that helps us find the limit of a function trapped between two other functions. This quiz will challenge your grasp of this theorem through a series of questions that range from basic definitions to more complex applications. Sharpen your calculus skills and see how well you understand the Squeeze Theorem!
We recommend that you do not leave the page that you are taking this quiz in. Stay honest 🙂
Squeeze Theorem Quiz Questions Overview
1. What is another name for the Squeeze Theorem?
Sandwich Theorem
Pinching Theorem
Compression Theorem
Boundary Theorem
2. Which of the following is a requirement for the Squeeze Theorem to be applicable?
The functions must be continuous.
The functions must be differentiable.
The functions must have the same limit at a point.
The functions must be integrable.
3. In the Squeeze Theorem, if f(x) ≤ g(x) ≤ h(x) for all x in an interval around c, and if lim(x→c) f(x) = L and lim(x→c) h(x) = L, what can we conclude about g(x)?
lim(x→c) g(x) = L
lim(x→c) g(x) = 0
lim(x→c) g(x) = ∞
lim(x→c) g(x) does not exist
4. Which of the following functions can be used to apply the Squeeze Theorem to find the limit of sin(x)/x as x approaches 0?
-1 ≤ sin(x) ≤ 1
cos(x) ≤ sin(x)/x ≤ 1
cos(x) ≤ sin(x) ≤ 1
0 ≤ sin(x)/x ≤ 1
5. If f(x) = x^2 sin(1/x) for x ≠ 0 and f(0) = 0, what is the limit of f(x) as x approaches 0?
0
1
Does not exist
∞
6. Which of the following statements is true about the Squeeze Theorem?
It can be used when the middle function is always greater than the upper function.
It requires the middle function to be always equal to the upper function.
It can be used when the middle function is squeezed between two other functions with the same limit.
It only applies to polynomial functions.
7. For which of the following limits can the Squeeze Theorem be applied?
lim(x→∞) (x^2 + 1)/x
lim(x→0) x^2 cos(1/x)
lim(x→0) (e^x – 1)/x
lim(x→∞) ln(x)/x
8. What is the limit of x^2 sin(1/x) as x approaches infinity?
0
1
Does not exist
∞
9. If g(x) = x^3 cos(1/x) for x ≠ 0 and g(0) = 0, what is the limit of g(x) as x approaches 0?
0
1
Does not exist
∞
10. Which of the following is a correct application of the Squeeze Theorem?
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = L and lim(x→c) h(x) = M, then lim(x→c) g(x) = (L + M)/2.
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = L and lim(x→c) h(x) = L, then lim(x→c) g(x) = L.
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = L and lim(x→c) h(x) = M, then lim(x→c) g(x) = L + M.
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = L and lim(x→c) h(x) = L, then lim(x→c) g(x) = 0.
11. What is the limit of (x^2 * sin(1/x^2)) as x approaches 0?
0
1
Does not exist
∞
12. Which of the following is an incorrect application of the Squeeze Theorem?
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = 0 and lim(x→c) h(x) = 0, then lim(x→c) g(x) = 0.
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = L and lim(x→c) h(x) = L, then lim(x→c) g(x) = L.
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = L and lim(x→c) h(x) = M, then lim(x→c) g(x) = L.
If f(x) ≤ g(x) ≤ h(x) and lim(x→c) f(x) = 0 and lim(x→c) h(x) = 0, then lim(x→c) g(x) = 0.
13. What is the limit of (x^2 * cos(1/x^2)) as x approaches infinity?
0
1
Does not exist
∞
14. Which of the following functions can be bounded to apply the Squeeze Theorem?
x^3 sin(1/x)
e^x sin(x)
ln(x) sin(x)
x^2 sin(x)
We recommend that you do not leave the page that you are taking this quiz in. Stay honest 🙂